Tarea 6. Geolocalización

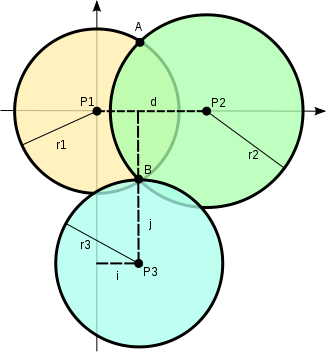
Para esta semana se pidió utilizar el algoritmo de geolocalización por triangulación. La trilateración es un método matemático para determinar las posiciones relativas de objetos usando la geometría de triángulos de forma análoga a la triangulación. 

La trilateración usa las localizaciones conocidas de dos o más puntos de referencia, y la distancia medida entre el sujeto y cada punto de referencia. Para determinar de forma única y precisa la localización relativa de un punto en un plano bidimensional usando sólo trilateración, se necesitan generalmente al menos 3 puntos de referencia.

Para realizar el código utilicé fragmentos de código de la página que está de referencia y también utilicé fórmulas que explican en Wikipedia.
 
Para esta tarea mi resultado fue el siguiente:

En este método lo que se hace es calcular la triateración entre los tres transmisores calculando el punto exacto donde se encuentra el receptor. La distancia entre dos puntos se calcula con la fórmula euclidiana entre dos puntos donde p1 representa la posicion del receptor mientras p2 la del transmisor. 

Referencias:
wwnick , John Austen, respuesta a nohat, "Trilateration using 3 latitude and longitude points, and 3 distances", "Geographic Information Systems", post creado en 22 de Julio 2011, http://gis.stackexchange.com/questions/66/trilateration-using-3-latitude-and-longitude-points-and-3-distances.